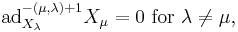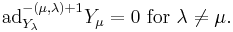Root system of a semi-simple Lie algebra
| Lie groups |
|---|
|
General linear group GL(n)
Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n) |
In mathematics, there is a one-to-one correspondence between reduced crystallographic root systems and semi-simple Lie algebras. We show the construction of a root system from a semi-simple Lie algebra and conversely, the construction of a semi-simple Lie algebra from a reduced crystallographic root system.
Contents |
Associated root system
Let g be a semi-simple complex Lie algebra. Let further h be a Cartan subalgebra of g, i.e. a maximal abelian subalgebra. Then h acts on g via simultaneously diagonalizable linear maps in the adjoint representation. For λ in h* define
We call a non-zero λ in h* a root if gλ is nontrivial. gλ is called the root space of λ. Obviously g0 = h. One can show that each non-trivial gλ is one-dimensional. Let R be the set of all roots. Since the elements of h are simultaneously diagonalizable, we have
The Cartan subalgebra h inherits an inner product from the Killing form on g. This induces an inner product on h*. One can show that with respect to this inner product R is a reduced crystallographic root lattice.
Associated semi-simple Lie algebra
Let E be a Euclidean space and R a reduced crystallographic root system in E. Let moreover Δ be a subset of positive roots. We define a complex Lie algebra over the generators
with the Chevalley-Serre relations
It turns out that the generated Lie algebra is semi-simple and has root system isomorphic to the given R.
Application
Due to the isomorphism, classification of semi-simple Lie algebras is reduced to the somewhat easier task of classifying reduced crystallographic root systems.
References
This article incorporates material from Root system underlying a semi-simple Lie algebra on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
- V.S. Varadarajan: Lie groups, Lie algebras, and their representations, GTM, Springer 1984.
![\mathfrak{g}_\lambda�:= \{a\in\mathfrak{g}: [h,a]=\lambda(h)a\text{ for all }h\in\mathfrak{h}\}.](/2012-wikipedia_en_all_nopic_01_2012/I/cc08e9c2748eba5d09b28433b57f32eb.png)
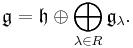
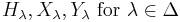
![[H_\lambda,H_\mu] =0 \text{ for all }\lambda,\mu\in\Delta](/2012-wikipedia_en_all_nopic_01_2012/I/f763093956b15714b1d66a570e9c14e6.png)
![[H_\lambda,X_\mu] = (\lambda,\mu)X_\mu,](/2012-wikipedia_en_all_nopic_01_2012/I/0ce4816c1d15e393c0e9f06bfcb1ee54.png)
![[H_\lambda,Y_\mu] = -(\lambda,\mu)Y_\mu,](/2012-wikipedia_en_all_nopic_01_2012/I/512584431db9b21a8e465dcb16736da6.png)
![[X_\mu,Y_\lambda] = \delta_{\mu\lambda}H_\mu,](/2012-wikipedia_en_all_nopic_01_2012/I/f3b227a140b5e7b773255ebc49aa5e76.png)